Matrice : Gauss-Jordan

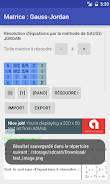
Gauss-Jordan APP သည် "Gaussian pivot" ဟုလည်းလူသိများသော Gauss-Jordan နည်းလမ်းကို အသုံးပြု၍ "n" အမည်မသိ ညီမျှခြင်းများကို ဖြေရှင်းရန် အစွမ်းထက်သောကိရိယာတစ်ခုဖြစ်သည်။ ၎င်းသည် ဒဿမများ၊ ကိန်းပြည့်များနှင့် အပိုင်းကိန်းများ အပါအဝင် အမျိုးမျိုးသော ဂဏန်းဖော်မတ်များကို ကိုင်တွယ်ပေးကာ အပိုင်းကိန်းနှင့် ဒဿမပုံစံနှစ်မျိုးလုံးအတွက် ရလဒ်များကို ပေးဆောင်သည်။ အပလီကေးရှင်းသည် ဖြေရှင်းချက်လုပ်ငန်းစဉ်၏ အသေးစိတ်အချက်အလက်များကို အဆင့်ဆင့်ရှင်းပြပေးထားပြီး အရင်းခံတွက်ချက်မှုများကို နားလည်ရလွယ်ကူစေသည်။ အသုံးပြုသူများသည် ရလဒ်များကို အနာဂတ်အကိုးအကားအတွက် ပုံများအဖြစ် သိမ်းဆည်းနိုင်သည်။

ညီမျှခြင်းဖြေရှင်းခြင်းအပြင် Gauss-Jordan APP သည် ပေးထားသောအမှတ်များပေါ်မူတည်၍ ကိန်းဂဏန်းညီမျှခြင်းများကို တွက်ချက်နိုင်ပြီး၊ ရုပ်ပုံဖော်ပြမှုအတွက် သက်ဆိုင်သောဂရပ်ကိုပြသထားသည်။ ၎င်းတွင် အပိုင်းခွဲရိုးရှင်းခြင်းနှင့် ကိန်းပြည့်ပြိုကွဲခြင်းကဲ့သို့သော ထပ်လောင်းအင်္ဂါရပ်များ ပါဝင်သည်။

ဤသည်မှာ Gauss-Jordan APP ၏ အဓိကအားသာချက်များ အကျဉ်းချုပ်ဖြစ်ပါသည်-

• ပြီးပြည့်စုံသောညီမျှခြင်းဖြေရှင်းခြင်း- Gauss-Jordan နည်းလမ်းဖြင့် ဒဿမများ၊ ကိန်းပြည့်များနှင့် အပိုင်းကိန်းများကို ပံ့ပိုးပေးသည့် Gauss-Jordan နည်းလမ်းကို အသုံးပြု၍ အမည်မသိ "n" ညီမျှခြင်းများကို ဖြေရှင်းပေးပါသည်။
အပိုင်းကိန်းနှင့် ဒဿမ နှစ်ခုလုံးအတွက် ရလဒ်များကို ပေးသည်။ ဖော်မတ်များ။
• တစ်ဆင့်ပြီးတစ်ဆင့် လမ်းညွှန်ချက်-
ပိုမိုနားလည်လာစေရန် ဖြေရှင်းချက်လုပ်ငန်းစဉ်အသေးစိတ် ရှင်းပြချက်များကို ပေးသည်။
• ရလဒ် သိမ်းဆည်းခြင်း-
အသုံးပြုသူများအား ခွင့်ပြုသည် ရလဒ်များကို လွယ်ကူစွာ ရယူအသုံးပြုနိုင်ရန်နှင့် မျှဝေရန်အတွက် ပုံများအဖြစ် သိမ်းဆည်းပါ။
• Polynomial Equation တွက်ချက်မှု-
ပေးထားသော အမှတ်များပေါ်မူတည်၍ ကိန်းဂဏန်းများ ညီမျှခြင်းများကို တွက်ချက်ပြီး သက်ဆိုင်ရာ ဂရပ်ကို ပြသသည်။
• နောက်ထပ် အင်္ဂါရပ်များ-
အပိုင်းများကို ရိုးရှင်းစေပြီး ထပ်တိုးလုပ်ဆောင်နိုင်စွမ်းအတွက် ကိန်းပြည့်များကို ပြိုကွဲစေသည်။
• Gauss-Jordan APP သည် အသုံးပြုသူအတွက် အဆင်ပြေစေပါသည်။ အင်တာဖေ့စ်နှင့် အပိုင်းကိန်းများ၊ ဒဿမများ၊ နှင့် ကိန်းပြည့်များနှင့် ညီမျှခြင်းများကို ဖြေရှင်းရန်အတွက် ပြည့်စုံသောအင်္ဂါရပ်အစုံအလင်။ ဤစွယ်စုံရကိရိယာကို အသုံးပြု၍ ပျော်ရွှင်ပါ။

Matrice : Gauss-Jordan Screenshots