Matrice : Gauss-Jordan

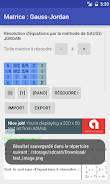
APP Gauss-Jordan ialah alat yang berkuasa untuk menyelesaikan persamaan dengan "n" yang tidak diketahui menggunakan kaedah Gauss-Jordan, juga dikenali sebagai "Gaussian pivot". Ia mengendalikan pelbagai format nombor, termasuk perpuluhan, integer dan pecahan, memberikan hasil dalam kedua-dua bentuk pecahan dan perpuluhan. Aplikasi ini menawarkan penjelasan langkah demi langkah terperinci tentang proses penyelesaian, menjadikannya mudah untuk memahami pengiraan asas. Pengguna juga boleh menyimpan keputusan sebagai imej untuk rujukan masa hadapan.

Di luar penyelesaian persamaan, APP Gauss-Jordan boleh mengira persamaan polinomial berdasarkan titik yang diberikan, memaparkan graf yang sepadan untuk perwakilan visual. Ia juga termasuk ciri tambahan seperti penyederhanaan pecahan dan penguraian integer.

Berikut ialah ringkasan kelebihan utama APP Gauss-Jordan:

• Penyelesaian Persamaan Komprehensif: Menyelesaikan persamaan dengan "n" yang tidak diketahui menggunakan kaedah Gauss-Jordan, menyokong perpuluhan, integer dan pecahan.
• Output Fleksibel: Memberikan hasil dalam kedua-dua pecahan dan perpuluhan format.
• Panduan Langkah demi Langkah: Menawarkan penjelasan terperinci tentang proses penyelesaian untuk pemahaman yang dipertingkatkan.
• Penjimatan Hasil: Membolehkan pengguna untuk simpan hasil sebagai imej untuk akses dan perkongsian mudah.
• Persamaan Polinomial Pengiraan: Mengira persamaan polinomial berdasarkan titik yang diberikan dan memaparkan graf yang sepadan.
• Ciri Tambahan: Memudahkan pecahan dan menguraikan integer untuk kefungsian tambahan.

APP Gauss-Jordan menyediakan antara muka mesra pengguna dan set komprehensif ciri untuk menyelesaikan persamaan, bekerja dengan pecahan, perpuluhan dan integer. Nikmati menggunakan alat serba boleh ini!

Matrice : Gauss-Jordan Screenshots