Matrice : Gauss-Jordan

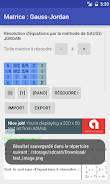
L'APP Gauss-Jordan è un potente strumento per risolvere equazioni con "n" incognite utilizzando il metodo Gauss-Jordan, noto anche come "pivot gaussiano". Gestisce vari formati numerici, inclusi decimali, numeri interi e frazioni, fornendo risultati sia in forma frazionaria che decimale. L'app offre una spiegazione dettagliata passo dopo passo del processo di soluzione, facilitando la comprensione dei calcoli sottostanti. Gli utenti possono anche salvare i risultati come immagini per riferimento futuro.

Oltre alla risoluzione delle equazioni, l'APP Gauss-Jordan può calcolare equazioni polinomiali basate su determinati punti, visualizzando il grafico corrispondente per la rappresentazione visiva. Include anche funzionalità aggiuntive come la semplificazione delle frazioni e la scomposizione dei numeri interi.

Ecco un riepilogo dei principali vantaggi dell'APP Gauss-Jordan:

• Risoluzione completa di equazioni: Risolve equazioni con "n" incognite utilizzando il metodo Gauss-Jordan, supportando decimali, numeri interi e frazioni.
• Output flessibile: Fornisce risultati sia in frazione che in decimale formati.
• Guida passo passo: Offre spiegazioni dettagliate del processo di soluzione per una migliore comprensione.
• Salvataggio dei risultati: Consente agli utenti di salva i risultati come immagini per un facile accesso e condivisione.
• Equazione polinomiale Calcolo: Calcola le equazioni polinomiali in base a determinati punti e visualizza il grafico corrispondente.
• Caratteristiche aggiuntive: Semplifica le frazioni e scompone i numeri interi per funzionalità aggiuntive.

L'APP Gauss-Jordan fornisce un'interfaccia intuitiva e un set completo di funzionalità per risolvere equazioni, lavorando con frazioni, decimali e numeri interi. Divertiti a usare questo strumento versatile!

Matrice : Gauss-Jordan Screenshots